The Two’s complement method is used to find a given decimal or a binary number. You can convert the 4, 8, 12, and 16 by the bit representation. The Two’s complement is a technique to store integers and make common math problems simple. The Two’s complement is used on the binary number and assists in computing. You can use the two’s complement calculator to find 2 complements of binary numbers like 50,100, 200, etc. This makes it simple to store the number and you can use it in the future:
Visit this link to use the best calculator
https://calculator-online.net/twos-complement-calculator/
How to determine two’s complement?
Now you need to find the two’s compliment of the number “50”:
Step1:
In the first step you need to convert the decimal number to a binary number:
(50)10 = (00110010)2
In this case the decimal number is “50” when you have converted into the binary number, it would be “00110010”.
Step2:
In the second step convert each 0 to 1 and 1 to 0.
(00110010)2 = 11001101
You may figure out that 00110010 and 11001101 are mirror images of each other
Step3:
In the third step, just take the answer of the second step, in this case, it is 11001101 add 1 to it.
11001101+1= 11001110
The Two’s complement of (50)10 = 11001110
You can use the calculator-online.net to find the Two’s complement of any decimal number.
Two complements of various numbers:
You can find the two complements of various numbers by the two’s complement calculator. In the following table, we have described various binary number and their answer.
| 2’s complement of -15 | 00001111 |
| 2’s complement of -7 | 0000111 |
| 2s complement of 15 | 11110001 |
| 2’s complement of -17 | 00010001 |
| 2’s complement of 4 | 11111100 |
| 2s complement of 6 | 11111010 |
Why use the 2’s complement?
2’s complement is utilized to perform various arithmetic operations and to store data in a binary form. The positive numbers are simply denoted by their magnitude, but when you are going to store the negative numbers then you may need to use 2’s complement technique.
Example 1:
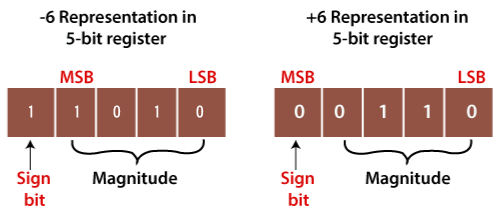
Now consider you need to store +6 and -6, both numbers are binary. You need to store these numbers using a 5-bit register.
- +6 is stored in the 5-bit register as 0 0110
Now for storing -6 represented in the 5-bit register, you need to follow the procedure:
How to store -6?
You can represent +6 is represented in the 5-bit register as 0 0110.
The -6 is represented in the 5-bit register:
- +6=0 0110, we know that +6=0 0110
- Now, find the 2’s complement of the number 0 0110, i.e. 1 1001 by the 2’s complement calculator.
- add 1 to 0 0110. The new binary number was generated in 11010. Here, we use the sign bit as one which means a number is a negative number.
Example 2:
Let’s consider that you are going to represent +120 and -120 by the two complement methods. You need an 8-bit register, for storing the data, you can store it in the 8-bit register by the two’s complement calculator.
- +120 is stored in the 8-bit register as 0 1111000.
How to store -120?
- +120 is 0 1111000
- 1’s complement of the number 0 1111000, i.e. 1 0000111.
- Now, add 1 to the number 1 0000111, the new number is 1 0001000. The first digit is 1, which means a number is a negative number.
Conclusion:
The two’s complement is commonly used in calculators and computers to manipulate ordinary numbers for various purposes to use them to store data in binary form. You can find the 2’s complement of negative and positive numbers by the two’s complement calculator
